Active learning for fast discovery of materials with targeted properties

07 September 2020

Designing new materials with targeted properties is often a long process, as there can be huge numbers of possible compositions and researchers often solely rely on their experience and on trial-and-error testing to find the right ones. Xue et al. wrote an article titled "Accelerated search for materials with targeted properties by adaptive design", in which they described how they tried to obtain NiTi-based shape-memory alloys with very low thermal hysteresis. They calculated that there were ~800 000 potential alloys in their search space. With no efficient physical models and simulation tools available to them, finding the desired alloy could have been a struggle. Fortunately, a solution was rapidly found thanks to active learning.

Active learning is an iterative process during which a machine learning algorithm "requests" the acquisition of new data in order to achieve some optimization objectives and to improve the quality of its machine learning model. The first step of this process is assembling an initial dataset. For more information on which sources of data can be used for this first step, read our last blog post: "The different sources of data that can used for machine learning applied to chemistry or materials R&D". After the initial dataset has been built, a machine learning model is trained with it. The optimization algorithm will then suggest experiments aimed at achieving the optimization objectives. Then, the suggested experiments are performed in a laboratory and the result of these experiments are added to the dataset. This iterative process is repeated until the objectives are reached, as depicted in the figure below.

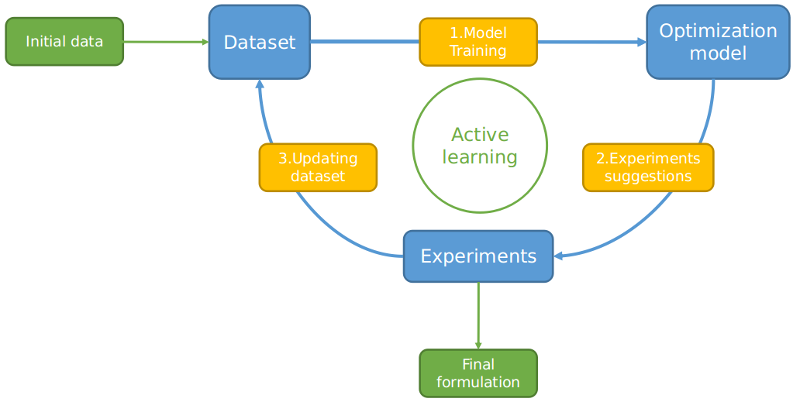
In this blog article, we will summarize how Xue et al. used active learning to find several new shape-memory alloys in only 36 experiments.

Problem

Shape-memory alloys have an interesting property: they can be deformed when cold but will go back to their original shape when heated. The shape memory effect arises from the transformation from an austenite phase (at high temperatures) to a martensite phase (at low temperatures). As the transformation temperatures do not coincide between cooling and heating, there is a thermal hysteresis ΔT and this ΔT can result in fatigue in the material and lead to cracks. Therefore, minimizing ΔT is of high importance for the durability of such alloys.

To reduce the potential number of alloys to test, the authors restrained the problem to the Ni_50-x-y-zTi₅₀Cu_xFe_yPd_z family which has showed promising results in previous studies. Therefore, their goal was to find a combination of x, y and z leading to the lowest ΔT possible. Even in this restricted search space, there were still 797 504 combinations that could be tested, making it extremely difficult to solve this problem. Therefore, the authors chose an innovative approach by using an active learning methodology to solve their problem.

Method

The authors' initial dataset contained 22 previously tested alloys. For each of these alloys, the dataset contained its composition, its ΔT and six calculated properties (known from prior knowledge to have an influence on ΔT): the valence electron number, the Pauling electronegativity, the pseudopotential radius, the metallic radius, the atomic radius and the Pettifor scale.

The authors compared various machine learning algorithms that can be used for active learning by performing cross-validation on the 22 initial samples. Cross-validation consists in splitting a dataset between a training set and a validation set. The training set is used to train a machine learning model while the validation set is used to check the accuracy of the predictions made by the model.

The results from the cross-validation tests showed that of the 10 regressor-selector combinations (the two components of the optimization algorithm) tested, the SVR_rbf-Knowledge Gradient combination gave the best results. This combination was therefore used in the active learning feedback loop.

The active learning loop that was designed consisted of several steps that can be repeated until an alloy with the targeted property is discovered. First, the dataset, consisting of the experimental results (Ni_50-x-y-zTi₅₀Cu_xFe_yPd_z and ΔT) and the calculated properties is used to train a regression model to predict the ΔT of each alloy from his composition and features. Then this model is used to predict the ΔT for each of the ~800 000 candidates. The best 4 candidates (with the lowest ΔT) are selected and tested. If the objective is not reached yet, the results can be added to the dataset and a new iteration can be performed.

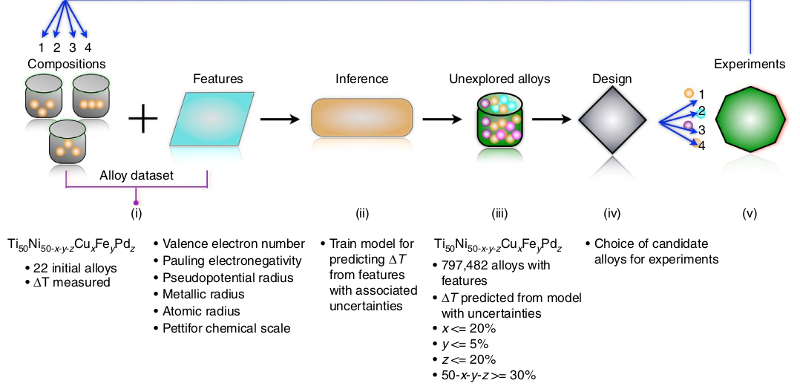
The experimental phase of this active learning process consisted in preparing ingots of the alloys suggested by the algorithms and then measuring their properties by DSC (Differential Scanning Calorimetry). The Ni_50-x-y-zTi₅₀Cu_xFe_yPd_z alloy ingots were prepared by arc-melting of 99.9% pure Ti, Ni, Cu, Fe and Pd in an argon atmosphere followed by post-treatments. Then the DSC measurements (with a rate of cooling/heating of 10 K/min) allowed to detect the martensitic transformation temperatures during cooling/heating and to measure ΔT (with ΔT = P_heating – P_cooling).

Results and conclusion

The feedback loop was performed 9 times in total, so 36 new alloys were produced and tested. The results are displayed in the plot below, where the measured ΔT and the ΔT that was predicted by the regression model are shown. The iteration n°0 shows the initial dataset of 22 alloys and each following iteration shows the results for the 4 alloys suggested by the optimization algorithm and tested.

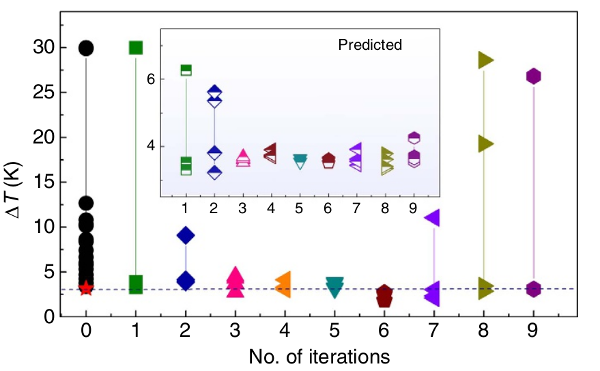
The best alloy from the initial 22 experiments had a ΔT of 3.15 K, while 14 out of the 36 new alloys showed a ΔT < 3.15 K, an impressive performance.

To check whether the use of active learning accelerated these discoveries, the authors calculated that if the alloys had been randomly chosen in the search space, the probability of finding 14 alloys with a ΔT < 3.15 K was equal to 3.7x10^-4. Therefore, the use of the active learning loop clearly allowed the authors to find memory-shape alloys much faster than with a traditional approach.

The authors noted that the alloys that were obtained with the design loop had a very low ΔT but high transformation temperatures. They would have preferred alloys with low transformation temperatures, but the optimization algorithm was not capable of managing two optimization objectives at the same time. A possible improvement would be to use an algorithm capable of performing multi-objective optimization.

If you want to use active learning to accelerate your R&D projects, our platform ChemAssistant™ offers a solution to perform multi-objective optimization in an easy and effective way, thanks to its smart and intuitive interface. Please contact us for further information about our ChemAssistant™ platform.